Every move in go always has two types of effect. The first type is the direct gain of the move, like when capturing a few stones. The second type is the threat of the move, actions that become possible because of the move. Although difficult in practice, in principle both types of effect can be expressed in points, this is one of the beauties of go.
We all know two kinds of moves: sente and gote. Sente moves often have a small direct gain, but certainly have a threat worth quite some points. That is why we feel obliged to answer these moves, to handle the threat. Gote moves may have a big direct gain, but there is hardly any threat worth thinking about at the moment the move is played.
There is a third kind of moves though, hardly anybody seems to talk about it. You see these kind of moves often in the opening and middle game. These moves both have a reasonable direct gain, and have a reasonable threat, that you may, or may not want to handle right away. You may call that threat the follow-up of the move. Quite often the handling of this kind of moves is difficult, as both gain and follow-up are not clear cut. Could it be that AlphaGo is the master at handling these kind of moves?
I have constructed the position shown with a few third kind moves, where the values of both gains and threats are totally clear. It looks like a late endgame, but you could treat this position as a model of the middle game, where a few alternatives have to be thought through. The sequences of moves are quite short, yet it is not at all easy to find out which is the best sequence when Black starts or when White starts. You might give this position a try, and in the meantime think about those strange moves of the third kind.
Kind regards,
Paul

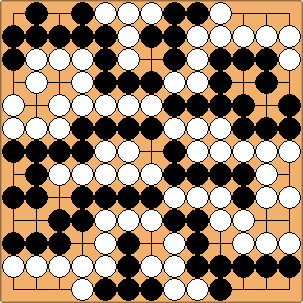
In the position you will notice that at the bottom there is kind of a double sente situation, at the top there is kind of a sente situation for Black and gote situation for White, and in the centre there is a double gote situation. Kind of sente, not sente: the threats are big but they are of about the same size as the direct gain of the moves. So the question arises: how forcing are these so-called sente moves?
Determining the best order of moves is quite difficult, you need to analyze all variations, working backwards, selecting the White move that gives the best result for White, and then selecting the previous Black move that gives the best result for Black, and so on. There seems to be no reliable shortcut by looking at the size of the direct gain and the size of the threat, putting them together in some formula. While playing a game this is all the more difficult because the size of the direct gain and the threat are not that clear, and moves in the opening and middle game influence each other. Humans have to rely on best practices, proverbs, experience. Computers like AlphaGo have a huge advantage here, they can approximate the right choice by playing through lots of variations and choosing the move with the highest chance of winning.
Diagram 1. Black starts, best variation
Black's first move in diagram 1 combines a gain and a threat. White ignores this move, playing the other move that has a follow-up. What remains then, are three gote moves, to be played in the right order. Black wins with 15 points.
Diagram 2. Black starts, so-called sente all the way
Diagram 2 shows what happens if White answers Black's so-called sente moves docilely: the result is very much better for Black, he wins with 36 points. One should notice that the white moves, while being big, have no follow-up.
Diagram 3. Black starts, suboptimal variation
In diagram 3 Black starts with the other sente-like move. The best continuation makes Black win with 14 points, only slightly less than the best result of diagram 1. White again ignores Black's first move as in diagram 1.
With only slightly different values for the gains and threats concerned the result could have favoured the variation of diagram 3. This makes you wonder about the validity of the rule that a double sente move should be played before the sente move.
Diagram 4. White starts, best variation
The best variation when White starts is shown in diagram 4. White's first move is the only one with a follow-up. Black's best response happens to be the big gote move, maybe a bit surprising. White wins with 9 points.
Diagram 5. White starts, suboptimal variation
In diagram 5 Black answers at the top, the only move with a follow-up. But the best Black can do is slightly worse than diagram 4, White wins with 11 points.
Diagram 6. White starts, disastrous variation
In diagram 6 White starts with a move without follow-up, Black then grabs the only big move with the follow-up. The result is very bad for White, compared with diagram 4: Black wins with 13 points.
Some conclusions
The value of the gains and threats in the position shown were fairly big to be able to explain the issues, still the point difference in the results sometimes is surprisingly big. The different situations are the Black or the White start, and a good or a bad move. Because of this sizeable point difference it pays to look for some lessons learned.
As the position shown indicates one could say:
Professional players, and AlphaGo, give quite a good example on how to handle moves of the third kind. My guess is that it pays to study their games, with these questions in mind:
I hope you liked this little exposé.
Kind regards,
Paul
This is very easy to compute. The gote in the middle gives black +15 if B plays first, and -12 if W plays first. So it's 27 points in gote and has temperature (15+12)/2=13.5.
The top is gote for W, leaving -11, and if B plays first is becomes a gote between +33 and +10, so 23 points in gote (which is smaller than the center gote). We can approximate it as being worth (33+10)/2 = +21.5 mean value (and T=(33-10)/2=11.5), which gives a span from +21.5 to -11 of 32.5, which means this isn't actually sente but more like a 32.5 point gote which has temperature 16.25. (It's not full sente because the followup move is SMALLER than the initial move; for true sente the followup threat has to be at least as big.)
The "double sente" is a little more complicated, but if B plays first becomes a gote between +36 and +11, with mean value (36+11)/2 = 23.5 and temperature (36-11)/2 = 12.5, and if W plays first becomes a gote between -11 and -34, with mean value(-11-34)/2 = -22.5 and temperature 25/2 = 12.5. The span between +23.5 and -22.5 is 46, so neither side of this is fully sente either, and we can treat it as a gote between +23.5 and -22.5 with temperature 23.
Since all the moves are "gote-ish", we just always take the largest one.
The optimal sequence for B is to take the T=23 "double sente", then W takes the T=16.25 "reverse sente", B takes the T=13.5 gote in the middle, and W takes the remaining T=12.5 gote to live on the bottom.
The optimal sequence for W is to take the T=23 "double sente", then B takes the T=16.25 "sente", W takes the T=13.5 gote in the middle, B takes the T=12.5 gote living on the bottom, and W takes the last T=11.5 gote living on the top.
So to sum up, there is no sente anywhere in this problem, just a bunch of gotes whose precise values are easy to compute. And once the computation is done, both players can just always take the largest remaining one, which is what you do when there are only gotes left.
thak you
Hello Howard,
Thank you very much for your feedback: very interesting, and it is nice to have someone react to an article. However, there are some comments I would like to make about it.
Sente: this probably is a matter of definition. To me, a move is sente when it has to be answered locally, directly related to the sente move, to get the best result. Because of this, to me the threat of the sente move doesn't necessarily have to be bigger than the direct gain, although it most of the time will be. Like, if there are two moves left, the one with direct gain 7 and threat 6, the other with direct gain 2 and threat 3, the first move is sente to me, the second one not.
The idea of this article was to explore what happens if both the direct gain and the threat of a move are quite significant, of comparable size. It became clear that answering the threat of these moves, treating them as sente, is very disadvantageous, as shown in diagram 2 in the article. Because of the disastrous result of that diagram 2, I guess that the same conclusion can be drawn even if the threat is mildly bigger than the direct gain of a move. I suspect that many amateur players don't know this, and will treat these moves as sente. When replaying professional games, they might wonder why these professionals tenuki so often, and this will be all the more the case when replaying the AlphaGo - AlphaGo games. So yes, these moves are gote as they are not sente by my definition: the problem one has to face in a real game, is to find a proper tenuki move when the opponent played such a third kind move, where the position in this article just gives you a few clear alternatives to choose from.
The method of calculation you used may come in handy as a shortcut, and it gives the right result for the position in the article. But I think it is incorrect, as sometimes it doesn't support the choice of the best move. The problem is that the method uses averages to calculate the temperature of a move. But the value of the move actually played, the gain accomplished, and foremost the threat materialized or countered, is not a result based on an average, there is a distinct choice between alternatives. The problem of the method occurs sometimes when the one move has a bigger direct gain and a smaller threat than the other move. To illustrate this, I modified the position, see below: the method suggests Black to start at the bottom, where a start at the top is better for Black.
Diagram 1. Modified position
In diagram 2, the players' gain per move is resp. B-6 (the captured stones at the top), W-13 (the captured stones at the bottom and the territory of the now safe group at the bottom left), B-31 (the killed group at the top right), W-12 (the captured stones at the centre) and B-2 (the territory of the now safe group at the bottom right). Thus Black has gained 39 points, White 25 points, the net result is 14 points for Black.
Diagram 2. Best sequence for Black
In diagram 3, the players' gain per move is resp. B-13 (the captured stones at the bottom and the territory of the now safe group at the bottom right), W-13 (the captured stones at the top and the territory of the now safe group at the top right), B-15 (the cut off stones at the centre) and W-2 (the territory of the now safe group at the bottom left). Thus Black has gained 28 points, White 15 points, the net result is 13 points for Black, which is 1 point worse than diagram 2.
Diagram 3. Inferior sequence for Black
I now explain my method of ranking moves, that comes close to yours. As said before, I think this method is incorrect.
For a side (Black, White) I count the direct gain of a move. Of the subsequent threat I count the gain for the one side if the threat materializes, and I count the gain for the other side if the threat is countered. I add these two values and devide the sum by two, as one doesn't really know who will play the follow-up move. This result is added to the direct gain of the move, to give some value of the move.
At the bottom for Black:
The direct gain is 13.
The two threat values (materialized and countered) are 24 and 2.
The value of black's move is 13 + ((24 + 2) / 2) = 26
At the top for Black:
The direct gain is 6.
The two threat values (materialized and countered) are 31 and 4.
The value of black's move is 6 + ((31 + 4) / 2) = 23,5
So, according to this method, the bottom scores higher than the top, but when playing the moves, starting at the top is better for Black.
I see no point in taking the part of White into consideration, as it is about what Black can accomplish. But if done, here the value for White at the bottom is higher than at the top too, adding to the misconception that it would be better for Black to start at the bottom.
To conclude, nothing beats comparing the results of sequences of moves, looking at all the gains per move, per player. This is terribly difficult to do for us humans, and quite more fitting for computers. That is one of the reasons why humans will never win again against the likes of AlphaGo.
Kind regards,
Paul
Isn't it just what you would call reverse sente ?
And when you say you see no point taking White's part into consideration, well, each player move in turn, so you have to...
Thanks
Which book did you use to become strong like that ?
I actually am not that strong a player, once was 1 kyu. But I put my mind to the problem, constructed positions that cannot be misjudged, and took on the horrifying task to work out the results of every variation, and "minimax" them. And then, I had to write an article about the subject, make sure the diagrams were right. I still feel proud about the result, all the more because I like the message it contains.