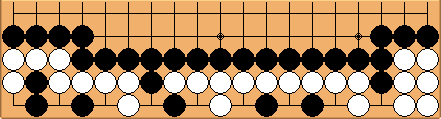
There are go proverbs that have a general applicability, like "Look for a move with several objectives" and "Look for a move with a good follow-up". That these proverbs make sense point-wise is illustrated by the position shown in diagram 1. At the right, there is a direct gain of 12 points. At the side, there is a direct gain of 3 points, but here is more going on.
Diagram 1
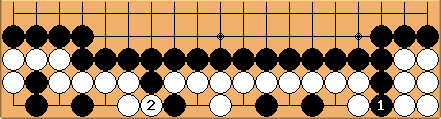
First, let's look at the position when Black starts. In diagram 2, Black takes the white stones, White cuts at the side. Black has 12 points, White 19 points, giving 7 points to White.
Diagram 2. Black moves first
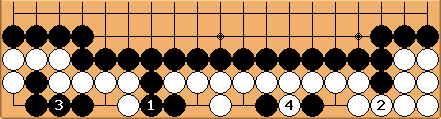
In diagram 3, Black connects at the side, and suddenly there are two additional follow-up situations, worth 8 and 6 points. White saves his stones at the right, Black makes a seki at the left, and White makes the only real territory. Black has 0 points, White has 6 points, giving 6 points to White, which is 1 point better for Black than diagram 2. This is remarkable, as the sum at the side of the direct gain and the largest follow-up is 11 points, smaller than the direct gain at the right of 12 points. This variation shows the power of the two proverbs when you combine them.
Diagram 3. Best for Black
Next, let's look at the position when White starts. In diagram 3, it seems logical that White cuts at the side, letting Black take the stones at the right. This way, the position is the same as in diagram 2, giving 7 points to White.
Diagram 4. White moves first
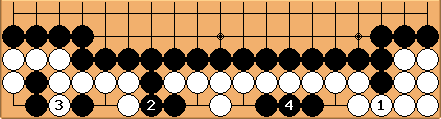
What happens if White connects at the right instead, shown in diagram 5? It is very gote, no follow-up at all. Black connects at the side like in diagram 3, but now it is White's turn, not Black's. So White takes the largest territory generating move at the left, leaving the seki at the right to Black. Black has 0 points, White has 8 points, giving 8 points to White, which is 1 point better for White than diagram 4. So, in this case, taking the direct gain at the right is better than preventing a move sequence with follow-up moves.
Diagram 5. Best for White
It is quite interesting to see a position where the best first move for Black is at another part of the board, and of a different type, than the best first move for White. In this simple made-up position it is rather easy to determine the best move to play, imagine however a real complex middle game position: one might never notice, unless an algorithm like AlphaGo takes a shot at it. Isn't go a magnificent game?
Kind regards,
Paul
