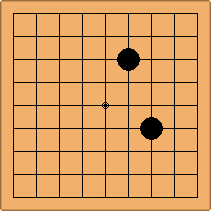
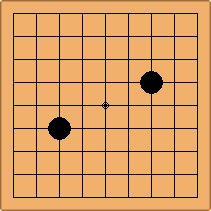
Many moves are possible to start the game. But centuries of human play and years of AI-Zero play show that starting with occupying the empty corners at either the 4-4 point or the 3-4 point is the most common. This is an indication that this way of playing might be the best for both players, you may call this the standard way of opening the game. Here in this article, a position after four moves is defined as being standard, if Black and White each occupied two empty corners with their first two moves, either at the 4-4 point or the 3-4 point. The question is, how many unique standard positions are there?
In this article, the positions are shown on a 9x9 board for space reasons, but they are applicable to any board size, including the standard 19x19 board.
Configurations and positions
One way to find out the number of unique positions, is to first look at the different configurations of two stones of one colour. Then, these configurations are combined into positions for the two colours, every configuration being applied to both the colours.
During this procedure, equivalent positions appear: they can be derived from positions already shown by mirroring or rotation. These equivalent positions are disregarded. The remaining non-equivalent positions are considered as being unique, although these positions can be mirrored and rotated to make them look differently.
There are two basic types of configuration: the parallel configuration, where the two stones of one colour are placed in two corners along a side of the board, and the diagonal configuration, where the two stones of one colour are placed in two corners along a diagonal of the board.
Conclusions
There are 69 unique positions when Black and White each occupy empty corners with their first two moves, either at the 4-4 point or the 3-4 point. 45 of them are in the parallel configuration, 24 of them in the diagonal configuration.
There are 2 unique positions when only 4-4 points are occupied, 52 of them when a combination of 4-4 and 3-4 points are occupied, and 15 of them when only 3-4 points are occupied.
A. The parallel configuration
The configurations of two stones of one colour
The configurations are shown at the right side of the board. These configurations can be shown at the other sides too, but they are equivalent to the configurations at the right side.
A1. Two 4-4 stones
There is 1 configuration, leading to 1 symmetric position: A1-1a.
A2. One 4-4 and one 3-4 stone
There are 2 configurations.
The first configuration is, the 3-4 stone facing the 4-4 stone. They can be laid out in 2 different ways on the board, exchanging the corners, leading to 2 equivalent asymmetric positions: A2-1a and A2-1b.
The second configuration is, the 3-4 stone not facing the 4-4 stone. They can be laid out in 2 different ways on the board, exchanging the corners, leading to 2 equivalent asymmetric positions: A2-2a and A2-2b.
A3. Two 3-4 stones
There are 3 configurations.
The first configuration is, both stones facing each other, leading to 1 symmetric position: A3-1a.
The second configuration is, both stones not facing each other, leading to 1 symmetric position: A3-2a.
The third configuration is, one stone facing the other while the other stone not facing the one. They can be laid out in 2 different ways on the board, exchanging the corners, leading to 2 equivalent asymmetric positions: A3-3a and A3-3b.
The combination of configurations for the two colours
To start with, the positions are shown with Black at the right side and White at the left side. These positions can be shown with Black and White at the other sides too, but they are equivalent to the positions shown. However, when switching colours leads to non-equivalent positions, the switched position shows White at the right side, for easy comparison with the unswitched position.
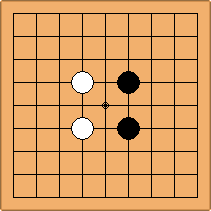
A1-1a and A1-1a
There is 1 symmetric position for both colours, combining into 1 unique position. There are equivalent positions when switching colours, leading to 1 unique position.
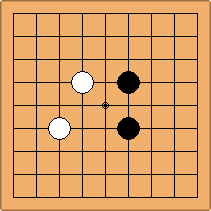
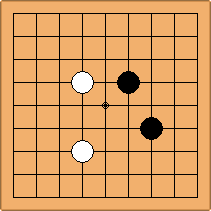
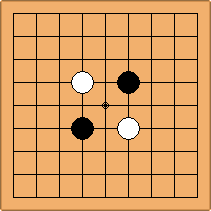
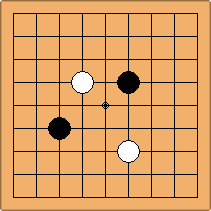
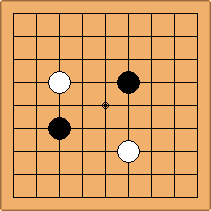
A1-1a and A2-1a/b
There is 1 symmetric position for one colour, and 2 asymmetric positions for the other colour, combining into 1 unique position. There are non-equivalent positions when switching colours, leading to 2 unique positions.
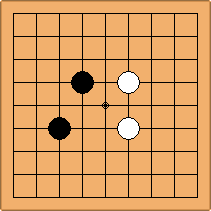
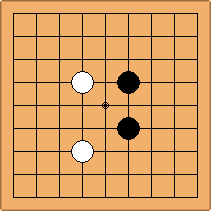
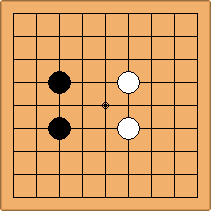
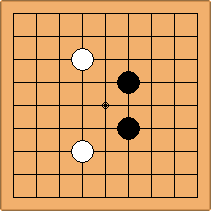
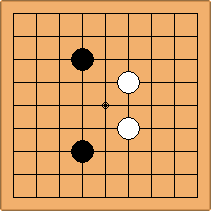
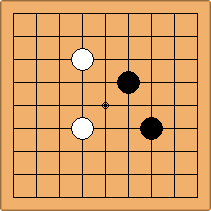
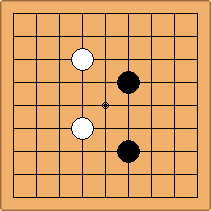
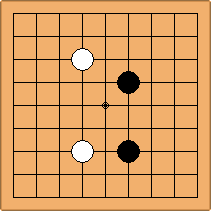
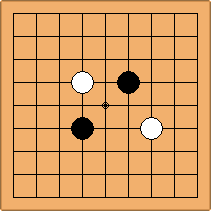
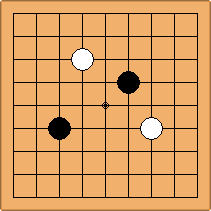
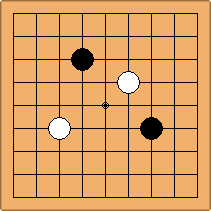
A1-1a and A2-2a/b
There is 1 symmetric position for one colour, and 2 asymmetric positions for the other colour, combining into 1 unique position. There are non-equivalent positions when switching colours, leading to 2 unique positions.
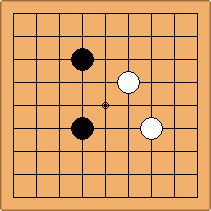
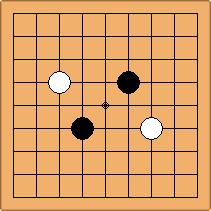
A1-1a and A3-1a
There is 1 symmetric position for both colours, combining into 1 unique position. There are non-equivalent positions when switching colours, leading to 2 unique positions.
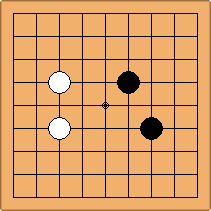
A1-1a and A3-2a
There is 1 symmetric position for both colours, combining into 1 unique position. There are non-equivalent positions when switching colours, leading to 2 unique positions.
A1-1a and A3-3a/b
There is 1 symmetric position for one colour, and 2 asymmetric positions for the other colour, combining into 1 unique position. There are non-equivalent positions when switching colours, leading to 2 unique positions.
A2-1a/b and A2-1a/b
There are 2 asymmetric positions for both colours, combining into 2 unique positions. There are equivalent positions when switching colours, leading to 2 unique positions.
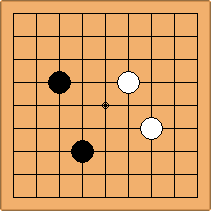
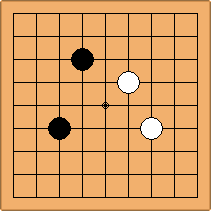
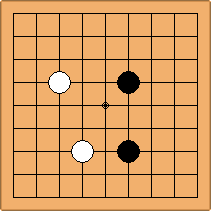
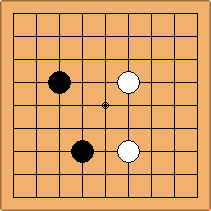
A2-1a/b and A2-2a/b
There are 2 asymmetric positions for both colours, combining into 2 unique positions. There are non-equivalent positions when switching colours, leading to 4 unique positions.
A2-1a/b and A3-1a
There are 2 asymmetric positions for one colour, and 1 symmetric position for the other colour, combining into 1 unique position. There are non-equivalent positions when switching colours, leading to 2 unique positions.
A2-1a/b and A3-2a
There are 2 asymmetric positions for one colour, and 1 symmetric position for the other colour, combining into 1 unique position. There are non-equivalent positions when switching colours, leading to 2 unique positions.
A2-1a/b and A3-3a/b
There are 2 asymmetric positions for both colours, combining into 2 unique positions. There are non-equivalent positions when switching colours, leading to 4 unique positions.
A2-2a/b and A2-2a/b
There are 2 asymmetric positions for both colours, combining into 2 unique positions. There are equivalent positions when switching colours, leading to 2 unique positions.
A2-2a/b and A3-1a
There are 2 asymmetric positions for one colour, and 1 symmetric position for the other colour, combining into 1 unique position. There are non-equivalent positions when switching colours, leading to 2 unique positions.
A2-2a/b and A3-2a
There are 2 asymmetric positions for one colour, and 1 symmetric position for the other colour, combining into 1 unique position. There are non-equivalent positions when switching colours, leading to 2 unique positions.
diagram]
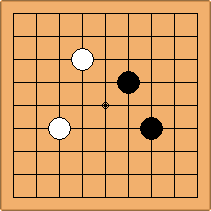
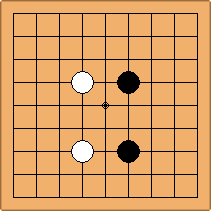
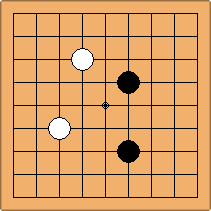
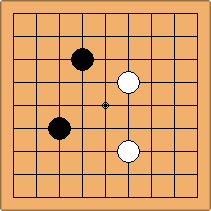
A2-2a/b and A3-3a/b
There are 2 asymmetric positions for both colours, combining into 2 unique positions. There are non-equivalent positions when switching colours, leading to 4 unique positions.
A3-1a and A3-1a
There is 1 symmetric position for both colours, combining into 1 unique position. There are equivalent positions when switching colours, leading to 1 unique position.
A3-1a and A3-2a
There is 1 symmetric position for both colours, combining into 1 unique position. There are non-equivalent positions when switching colours, leading to 2 unique positions.
A3-1a and A3-3a/b
There is 1 symmetric position for one colour, and 2 asymmetric positions for the other colour, combining into 1 unique position. There are non-equivalent positions when switching colours, leading to 2 unique positions.
A3-2a and A3-2a
There is 1 symmetric position for both colours, combining into 1 unique position. There are equivalent positions when switching colours, leading to 1 unique position.
A3-2a and A3-3a/b
There is 1 symmetric position for one colour, and 2 asymmetric positions for the other colour, combining into 1 unique position. There are non-equivalent positions when switching colours, leading to 2 unique positions.
A3-3a/b and A3-3a/b
There are 2 asymmetric positions for both colours, combining into 2 unique positions. There are equivalent positions when switching colours, leading to 2 unique positions.
B. The diagonal configuration
The configurations of 2 stones of one colour
The configurations are shown along the diagonal from the upper right corner to the lower left corner of the board. These configurations can be shown along the other diagonal too, but they are equivalent to the configurations along the diagonal from the upper right corner to the lower left corner.
B1. Two 4-4 stones
There is 1 configuration, leading to 1 symmetric position: B1-1a.
B2. One 4-4 and one 3-4 stone
There is 1 configuration. The stones can be laid out in 4 different ways on the board, exchanging the corners and mirroring along the diagonal, leading to 4 equivalent asymmetric positions: B2-1a to B2-1d.
B3. Two 3-4 stones
There are 2 configurations.
The first configuration is, both stones facing the same corner. They can be laid out in 2 different ways on the board, mirroring along the diagonal, leading to 2 equivalent symmetric positions: B3-1a and B3-1b.
The second configuration is, both stones not facing the same corner. They can be laid out in 2 different ways on the board, mirroring along the diagonal, leading to 2 equivalent symmetric positions: B3-2a and B3-2b.
The combination of configurations for the two colours
To start with, the positions are shown with Black along the diagonal from the top right corner to the bottom left corner, and White along the other diagonal. These positions can be shown with Black and White reversing diagonals too, but they are equivalent to the positions shown. However, when switching colours leads to non-equivalent positions, the switched position shows White along the diagonal from the top right to the bottom left, for easy comparison with the unswitched position.
B1-1a and B1-1a
There is 1 symmetric position for both colours, combining into 1 unique position. There are equivalent positions when switching colours, leading to 1 unique position.
B1-1a and B2-1a/d
There is 1 symmetric position for one colour, and 4 asymmetric positions for the other colour, combining into 1 unique position. There are non-equivalent positions when switching colours, leading to 2 unique positions.
B1-1a and B3-1a/b
There is 1 symmetric position for one colour, and 2 symmetric positions for the other colour, combining into 1 unique position. There are non-equivalent positions when switching colours, leading to 2 unique positions.
B1-1a and B3-2a/b
There is 1 symmetric position for one colour, and 2 symmetric positions for the other colour, combining into 1 unique position. There are non-equivalent positions when switching colours, leading to 2 unique positions.
B2-1a/d and B2-1a/d
There are 4 asymmetric positions for both colours, combining into 4 unique positions. For 2 of them there are equivalent positions when switching colours. For the other 2 there are non-equivalent positions when switching colours, but the switched position of the one is equivalent to the unswitched position of the other. This all, leading to 4 unique positions.
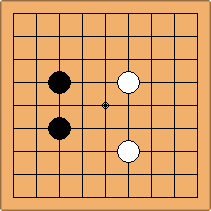
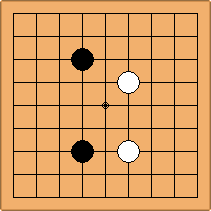
B2-1a/d and B3-1a/b
There are 4 asymmetric positions for one colour, and 2 symmetric positions for the other colour, combining into 2 unique positions. There are non-equivalent positions when switching colours, leading to 4 unique positions.
B2-1a/d and B3-2a/b
There are 4 asymmetric positions for one colour, and 2 symmetric positions for the other colour, combining into 2 unique positions. There are non-equivalent positions when switching colours, leading to 4 unique positions.
B3-1a/b and B3-1a/b
There are 2 symmetric positions for both colours, combining into 1 unique position. There are equivalent positions when switching colours, leading to 1 unique position.
B3-1a/b and B3-2a/b
There are 2 symmetric positions for both colours, combining into 1 unique position. There are non-equivalent positions when switching colours, leading to 2 unique position.
B3-2a/b and B3-2a/b
There are 2 symmetric positions for both colours, combining into 2 unique positions. There are equivalent positions when switching colours, leading to 2 unique positions.

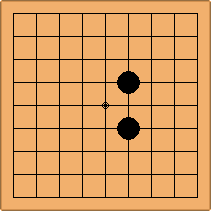
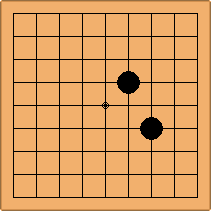
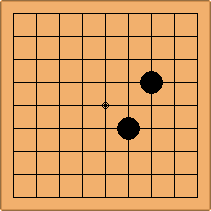
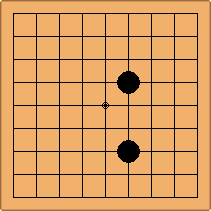
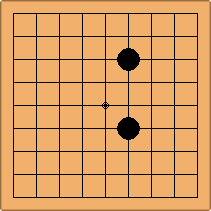
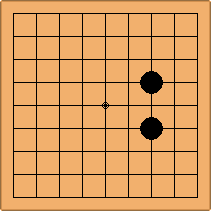
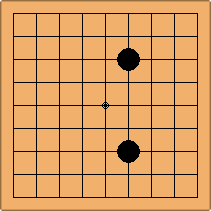
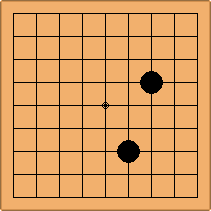


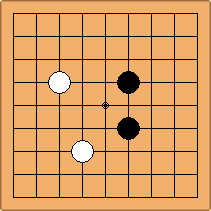
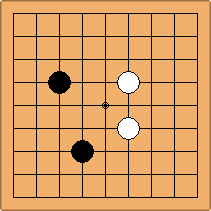
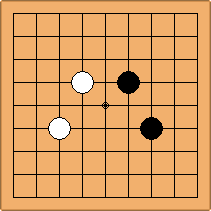
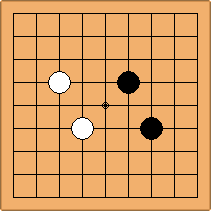

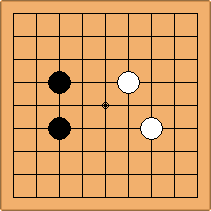
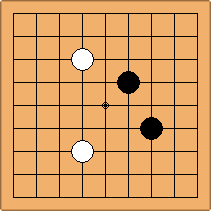
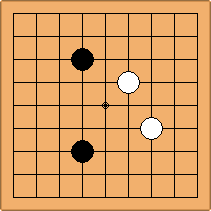
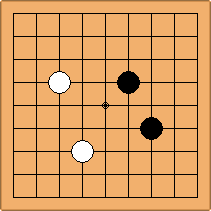

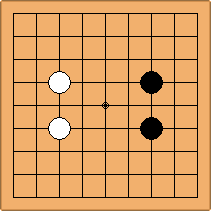
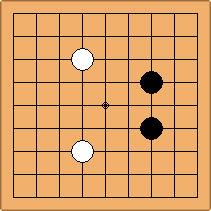
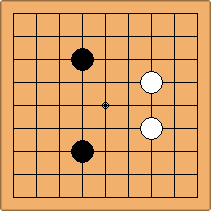
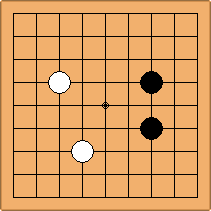
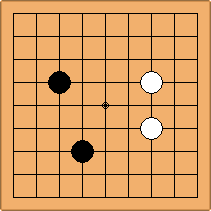
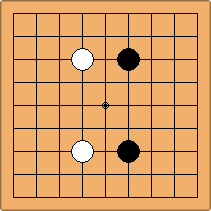
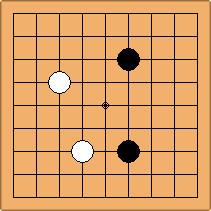

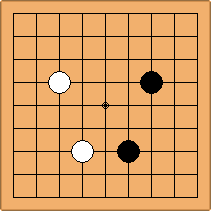
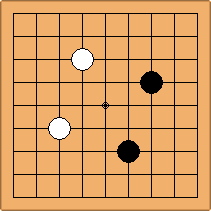



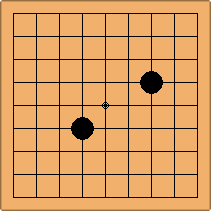
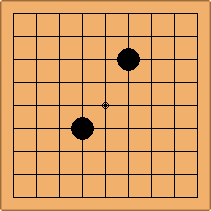

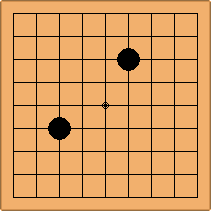




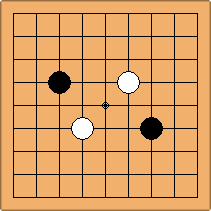
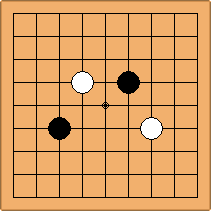
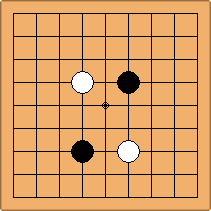
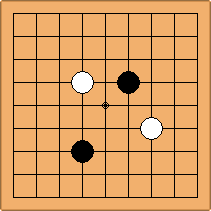
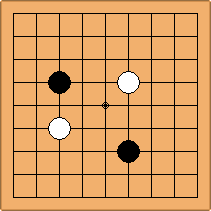
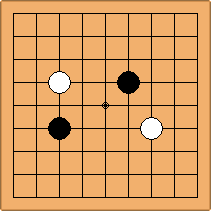
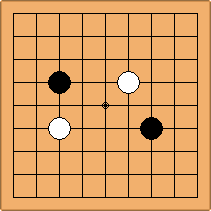
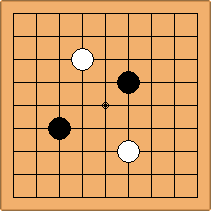
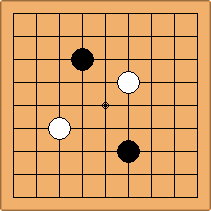
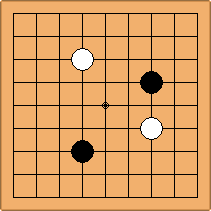
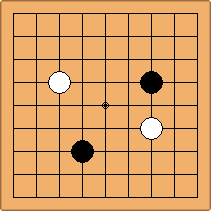
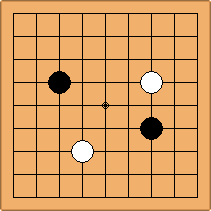
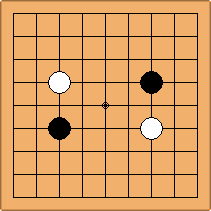
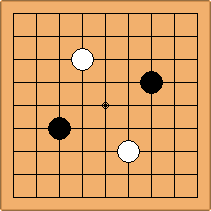
If 3-3 and 5-3 are included the number goes up to close to 3000 different openings.